Vou tentar explicar como fazer multiplicações utilizando o método japonês. É bastante simples e muito interessante, pelo menos para mim! 🙂
Vejamos então como funciona:
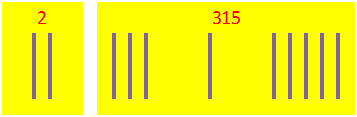
Para cada um dos operadores, desenha um número correspondente de linhas. Um operador em linhas verticais e o outro em linhas horizontais. Agrupa as linhas de acordo com o “valor” de cada dígito. Por exemplo: para “2”, desenha duas linhas; para “315”, desenha um conjunto de três linhas, um conjunto de uma linha e um conjunto de cinco linhas. Algo do género:
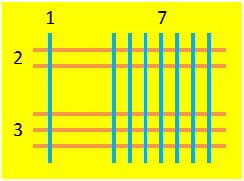
Faz o mesmo para o outro operador, mas agora com linhas horizontais. As linhas dos operadores devem ficar sobrepostas. Por exemplo, se quiséssemos fazer a multiplicação 23×17 teríamos algo do género:
Como para (quase) tudo há regras, aqui também tem de as haver. Mas são muito simples:
1- Contámos o número de vezes que as linhas se cruzam;
2- Se houver mais de um grupo de cruzamentos, começamos por contar, em diagonal, do canto inferior direito para o canto superior esquerdo;
3- Se o resultado de uma soma for superior a 9, guardámos o dígito da direita e juntamos o da esquerda à soma da diagonal seguinte;
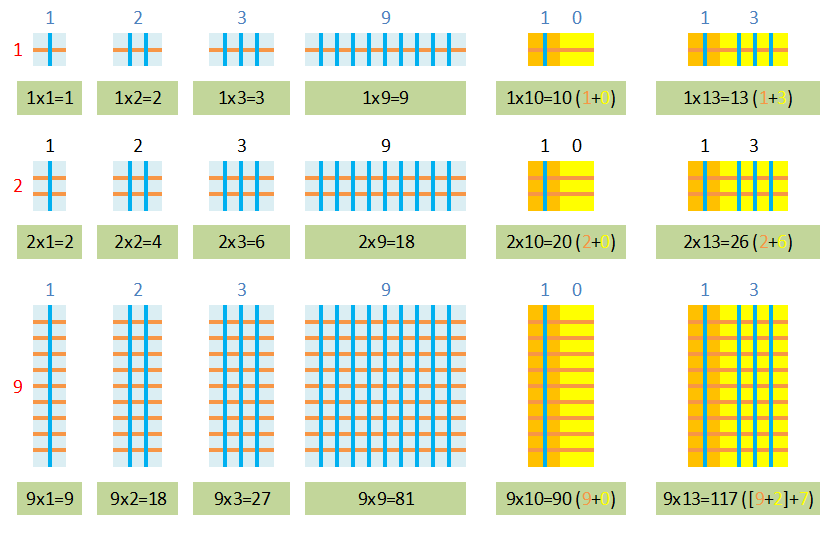
Simples, não é? Vejamos alguns exemplos:
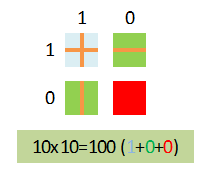
Deves ter em atenção o zero. Não desenhas a linha, mas tens de somar a sua intersecção, que no caso dará um resultado “0”. O exemplo a seguir mostra-te não só como lidar com o zero, como também o “esquema” das diagonais. Começas por somar o número de cruzamentos dos últimos dígitos, ou seja: o canto inferior direito, a vermelho. Neste caso temos zero cruzamentos pelo que guardamos o “0”. Passámos à diagonal seguinte, a verde. Neste caso também temos zero cruzamentos. Guardamos também este “0” e passámos a ter “00”. Vamos agora à diagonal seguinte que no exemplo corresponde ao primeiro bloco, a azul. Temos um cruzamento pelo que vamos guardar o “1”. Se o juntarmos ao que já tínhamos, passámos a ter “100”:
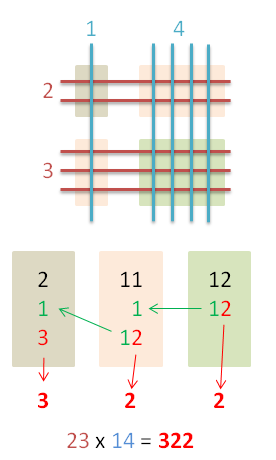
Agora alguns exemplos mais complexos. No próximo vamos multiplicar 23 por 14.
Na diagonal mais à direita (o grupo inferior direito) temos 12 cruzamento. Guardamos o 2 e passámos o 1 para a soma seguinte. Na diagonal seguinte temos: 8+3, o que dá 11. Juntando o 1 que vem da diagonal anterior, temos 12. Guardamos o 2 e passámos o 1 para a soma seguinte. Aqui temos dois cruzamentos, aos quais vamos juntar o 1 que trazíamos da operação anterior, o que dá 3. Passamos a ter guardados os valores: 3, 2 e 2. o resultado final é, portanto, 322. 23×14=322.
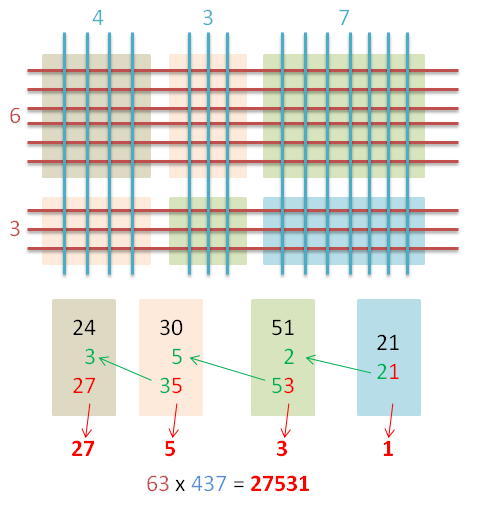
Segue o mesmo raciocínio para a operação seguinte: 63×437. Temos mais uma diagonal, mas o processo é o mesmo.
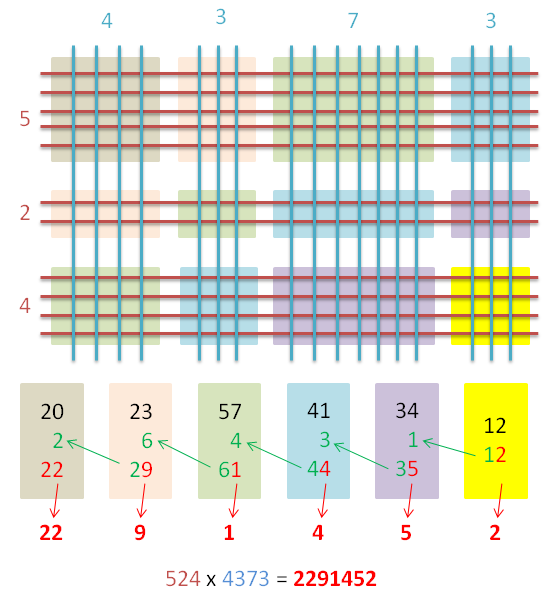
Ou um ainda mais complexo: 524×4373
Não importa o número de dígitos dos operadores, o processo é sempre o mesmo. Podes efectuar qualquer multiplicação. Deixa o teu comentário. Como comecei por dizer, este é um sistema japonês. Brevemente irei explicar outros sistemas.