Mês: Novembro 2013
joão estava farto da vida
Um dia resolveu enforcar-se numa árvore. Mas esta estava tão seca, mas tão seca, que o ramo partiu-se!
Depois, João atirou-se para a frente de um camião. Nada. O gajo travou a tempo!
Tentou com uma pistola. Encravou.
Pediu ajuda a um amigo. O amigo recusou.
Experimentou com veneno. Estava fora do prazo, ganhou uma diarreia tremenda.
Estava desesperado, tinha de encontrar uma solução infalível.
Ligou a televisão. Estava a dar um programa desportivo. “Já sei”, pensou.
Saiu, entrou no automóvel, e conduziu em direcção ao norte.
Chegou ao seu destino final. Num dia de jogo no estádio do Dragão a agitação era geral.
João foi-se entranhando na multidão, no meio da claque dos Super Dragões.
Quando estava bem no centro, gritou com toda a força que lhe restava:
QUERO QUE O PORTO SE FODA!!!
Descanse em paz!
O enterro é amanhã, às 15.30, na igreja da Luz.
simetria
1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
frase do dia
Se não puderes ajudar, atrapalha! O importante é participar!
os três porquinhos e o lobo mau (contada por um engenheiro)
O filho quer dormir e pede ao pai (engenheiro) para contar uma história e ele conta a dos três porquinhos.
Meu Filho, era uma vez três porquinhos (P1, P2 e P3) e um Lobo Mau, por definição, LM, que vivia para os atormentar.
P1 era esperto, estudava Engenharia Electrotécnica e já era formado em Engenharia Civil.
P2 era arquitecto e vivia em fúteis devaneios estéticos absolutamente desprovidos de cálculos rigorosos.
P3 estudava Comunicação e Expressão Visual.
LM, na Escala Oficial da Medição da Maldade (EOMM) era Mau nível 8,75 (arredondado a partir da 3ª casa decimal para cima). LM também era um grande investidor imobiliário sem escrúpulos e cobiçava a propriedade que pertencia aos Pn (onde “n” é um número natural e varia entre 1 e 3), visto que o terreno era de boa conformidade geológica e configuração topográfica, localizado próximo do ex-futuro aeroporto de Alcochete.
Mas nesse promissor perímetro P1 construiu uma casa de tijolos, sensata e logicamente planeada, toda protegida e com mecanismos automáticos.
Já P2 montou uma casa de blocos articulados feitos de mogno que mais parecia um castelo lego tresloucado.
Enquanto P3 planeou no Autocad e montou ele mesmo, com barbantes e poliestireno como fundamentos, uma cabana de palha com teto solar, e achava aquilo “o máximo”.
Um dia, LM foi até à propriedade dos suínos e disse, encontrando P3:
“Uahahhahaha, corra, P3, porque vou gritar, e vou berrar e chamar o Conselho de Engenharia Civil para denunciar a tua casa de palha projectada por um formando em Comunicação e Expressão Visual! ”
Ao ouvir isto, P3 correu para sua amada cabana, mas quando lá chegou já os fiscais do Conselho tinham deitado tudo abaixo. Então P3 correu para a casa de P2. E ao chegar lá encontrou LM à porta, a bater com força e a berrar:
“Abre esta porta, P2, ou vou gritar, gritar e berrar e chamar a Greenpeace, para denunciar que tu usaste madeira nobre de áreas não-reflorestadas e areia de praia para misturar no cimento.”
Antes que P2 alcançasse a porta, esta foi deitada abaixo por uma multidão ensandecida de eco-chatos que invadiram o ambiente, vandalizaram tudo e ocuparam os destroços, pixando e entoando palavras de ordem.
P3 e P2 correm para a casa de P1. Quando chegaram à casa de P1, este recebeu-os e os dois caíram ofegantes na sala de entrada.
P1: O que é que aconteceu?
P2: LM, lobo mau por definição, nível 8.75, destruiu nossas casas e desapropriou os terrenos.
P3: Não temos para onde ir. E agora, o que é que eu vou fazer? Sou apenas um formando em Comunicação e Expressão Visual!
Tum-tum-tum-tum-tuuummm!!!! (isto é somente uma simulação das batidas na porta, meu filho! o som correcto não é este.)
LM: P1, abre esta porta e assina este contrato de transferência de posse do imóvel, ou eu vou gritar e berrar e chamar os fiscais do Conselho de Engenharia! E se for preciso até chamo os gajos da ASAE!
Como P1 não abria (apesar da insistência covarde do porco arquitecto e do…do… comunicador e expressivo visual) LM chamou os fiscais e os gajos da ASAE, e estes fizeram testes de robustez do projecto, inspecções sanitárias, projecções geomorfológicas, exames de agentes físico-estressores, cálculos com muitos integrais, matrizes, e geometria analítica avançada. E não encontraram nada de errado. Então LM gritou e gritou e berrou ainda mais, e vieram os gajos da Greenpeace, mas todo o projecto e implementação da casa de P1 era ecologicamente correcto.
Cansado e esbaforido, o vilão lupino resolveu agir de forma irracional (porém super-comum nos contos de fadas): ele pessoalmente escalou a casa de P1 pela parede, subiu até à chaminé e resolveu entrar por esta para invadir a casa.
Mas quando saltou para dentro da chaminé, um dispositivo mecatrónico instalado por P1 captou a sua presença por um sensor térmico e activou uma catapulta que impulsionou com uma força de 33.300 N (Newtons) LM para cima.
Este subiu aos céus, numa trajectória parabólica estreita, alcançando o vértice, onde a sua velocidade chegou a zero, a 200 metros do chão.
Agora, meu filho, antes que tu mergulhes num sono repousado e o pai te cubra com este edredão macio e quente, admitindo que a gravidade vale 9,8 m/s² e que um lobo adulto médio pesa 60 kg, calcula:
a) o deslocamento no eixo “x”, tomando como referencial a chaminé.
b) a velocidade de queda de LM quando este tocou o chão e
c) o susto que o Lobo Mau apanhou, num gráfico lógico que varia do 0 (repouso) ao 9 (ataque histérico).
mercado de acções
Certo dia, numa aldeia do interior, apareceu um homem anunciando aos aldeões que compraria burros por 100€ cada. Os aldeões, sabendo que havia muitos burros selvagens na região, iniciaram a caça aos ditos. O homem comprou centenas de burros a 100€ e então os aldeões diminuíram a caça. Mas o homem anunciou que passaria a pagar 200€ por cada burro. Os aldeões renovaram os seus esforços e foram novamente à caça.
Os burros começaram a escassear cada vez mais e os aldeões a desistir da busca. A oferta aumentou para 250€ e a quantidade de burros ficou tão pequena que deixou de haver interesse na caça.
O homem anunciou, então, que compraria cada burro por 500€! Como tinha de ir à cidade, deixaria o seu assistente a cuidar da compra dos burros.
Na ausência do homem, o assistente disse aos aldeões: “Estão a ver todos estes burros que o homem vos comprou? Eu posso vendê-los por 350€ a vocês e quando o homem voltar da cidade, vocês podem vender-lhos por 500€ cada.”
Os aldeões, espertos, pegaram em todas as suas economias e compraram todos os burros ao assistente.
E nunca mais viram o homem ou seu assistente, somente burros por todos os lados.
Agora já deves ter percebido como é que funciona o mercado de acções!
a multiplicação: o sistema japonês
Vou tentar explicar como fazer multiplicações utilizando o método japonês. É bastante simples e muito interessante, pelo menos para mim! 🙂
Vejamos então como funciona:
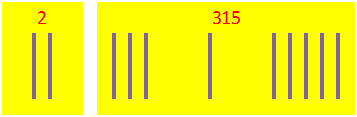
Para cada um dos operadores, desenha um número correspondente de linhas. Um operador em linhas verticais e o outro em linhas horizontais. Agrupa as linhas de acordo com o “valor” de cada dígito. Por exemplo: para “2”, desenha duas linhas; para “315”, desenha um conjunto de três linhas, um conjunto de uma linha e um conjunto de cinco linhas. Algo do género:
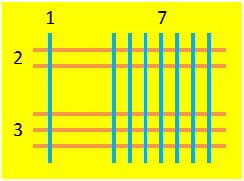
Faz o mesmo para o outro operador, mas agora com linhas horizontais. As linhas dos operadores devem ficar sobrepostas. Por exemplo, se quiséssemos fazer a multiplicação 23×17 teríamos algo do género:
Como para (quase) tudo há regras, aqui também tem de as haver. Mas são muito simples:
1- Contámos o número de vezes que as linhas se cruzam;
2- Se houver mais de um grupo de cruzamentos, começamos por contar, em diagonal, do canto inferior direito para o canto superior esquerdo;
3- Se o resultado de uma soma for superior a 9, guardámos o dígito da direita e juntamos o da esquerda à soma da diagonal seguinte;
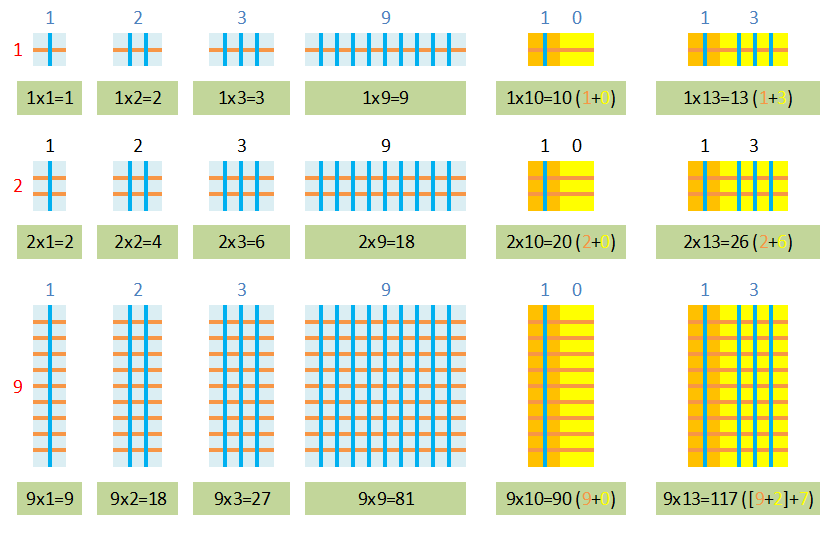
Simples, não é? Vejamos alguns exemplos:
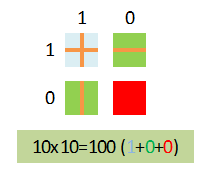
Deves ter em atenção o zero. Não desenhas a linha, mas tens de somar a sua intersecção, que no caso dará um resultado “0”. O exemplo a seguir mostra-te não só como lidar com o zero, como também o “esquema” das diagonais. Começas por somar o número de cruzamentos dos últimos dígitos, ou seja: o canto inferior direito, a vermelho. Neste caso temos zero cruzamentos pelo que guardamos o “0”. Passámos à diagonal seguinte, a verde. Neste caso também temos zero cruzamentos. Guardamos também este “0” e passámos a ter “00”. Vamos agora à diagonal seguinte que no exemplo corresponde ao primeiro bloco, a azul. Temos um cruzamento pelo que vamos guardar o “1”. Se o juntarmos ao que já tínhamos, passámos a ter “100”:
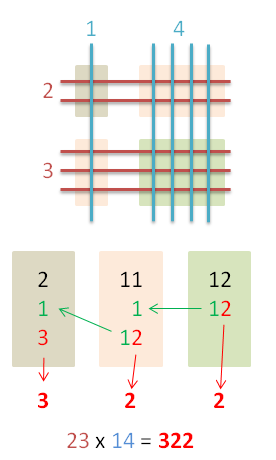
Agora alguns exemplos mais complexos. No próximo vamos multiplicar 23 por 14.
Na diagonal mais à direita (o grupo inferior direito) temos 12 cruzamento. Guardamos o 2 e passámos o 1 para a soma seguinte. Na diagonal seguinte temos: 8+3, o que dá 11. Juntando o 1 que vem da diagonal anterior, temos 12. Guardamos o 2 e passámos o 1 para a soma seguinte. Aqui temos dois cruzamentos, aos quais vamos juntar o 1 que trazíamos da operação anterior, o que dá 3. Passamos a ter guardados os valores: 3, 2 e 2. o resultado final é, portanto, 322. 23×14=322.
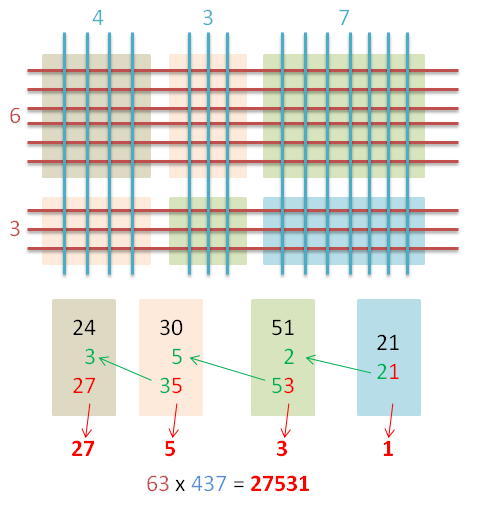
Segue o mesmo raciocínio para a operação seguinte: 63×437. Temos mais uma diagonal, mas o processo é o mesmo.
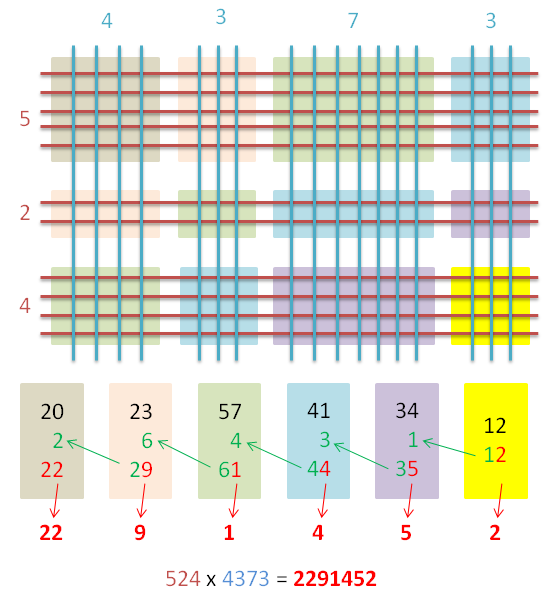
Ou um ainda mais complexo: 524×4373
Não importa o número de dígitos dos operadores, o processo é sempre o mesmo. Podes efectuar qualquer multiplicação. Deixa o teu comentário. Como comecei por dizer, este é um sistema japonês. Brevemente irei explicar outros sistemas.